Investigating line-breaking passes
Introduction
Line-breaking passes are widely discussed amongst football analysts, coaches and experts. As passes that dissect a line of the opposition’s formation, they usually allow a team to transition from one attacking phase to another.
Therefore a player’s ability to play a good line-breaking pass is highly valued. While some existing stats, like packing or progressive passes, might sometimes serve as a proxy, I have applied Stats Perform tracking data, taken from the 2018/19 Belgian Pro League, with the objective of creating a new method for directly measuring the value of these passes.
Defining a Line-Breaking Pass
The starting point of this research was to establish a reliable approach for detecting formation lines, taking into consideration that each player can switch from one formation line to another as a result of their movement.
A natural way to cluster players into lines is to apply a clustering algorithm onto the x coordinate of the pitch (the touchline coordinate). After testing a few clustering algorithms, I finally settled on using one of the simplest – a Jenks natural breaks optimisation – with three clusters being formed of outfield players (with the goalkeepers then forming a fourth cluster). This algorithm is an efficient and highly comprehensible technique to reduce the volume of deviation from the cluster mean.
To prevent immediate switching between lines, the x coordinate was averaged over a two-second time window. Additionally, groupings that lasted less than one second were removed and reassigned to the previous line.
Adopting a set number of clusters may not be the optimal approach for analysing other areas of football, but I found it acceptable when looking for line-breaking passes, as for the most part, this is how a defensive team would normally be set up. In addition, allowing for a variable number of clusters would likely lead to clusters consisting of one player who doesn’t really form a line, but cannot be ignored as their positioning may be crucial to the defensive set-up.
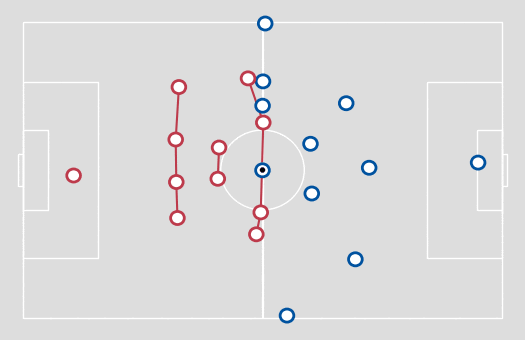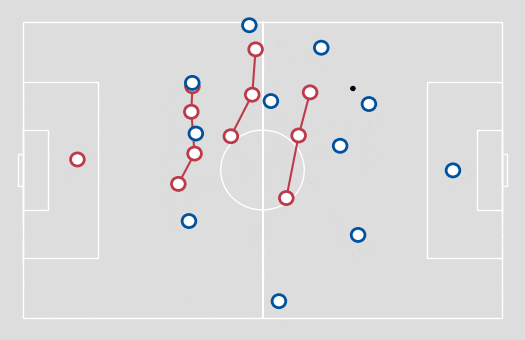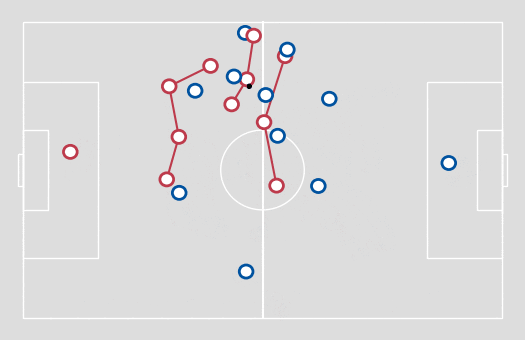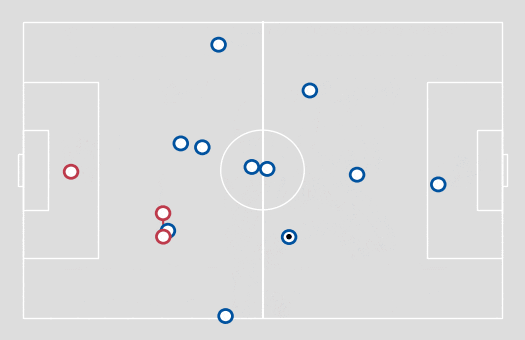
Figure 1. An example of formation line detection, using 1-D clustering.
For the purposes of this analysis, a line-breaking pass is defined as a pass which not only intersects at least one of the opposition lines in a geometric sense, but also:
– Progresses the ball forward at least 10 metres;
– Has a starting point which is at least five metres away from the point of intersection;
– Has an ending point of at least two metres beyond the deepest sitting player in the line.
This definition eliminates passes that:
– Break the lines in a geometric sense, but are unlikely to result in a transition to the next attacking phase;
– Are extremely easy to complete, due to their proximity to the line that it penetrates.
The definition also means that the receiver of a pass is not subject to pressure applied by any opposition player who was part of the broken line.
All open play passes were considered in the analysis, however as Z coordinates (ball height) were not part of the data sample, the findings do not take into account if a pass was played over the top or along the ground.
One final consideration before we move onto the model itself concerns the challenges of defining an intercepted pass. As the end coordinates of an interception points to the place on the field where the interception takes place, we cannot rely on them to determine whether a pass was meant to be line-breaking or not.
However, given we have information on the angle of the pass and the lower-bound of a pass length, we can try to infer the intended final destination of a pass. To do this, we apply the Weibull survival model, which is a technique specifically suited to deal with lower-bounded data, to estimate the expected additional length of a pass from the point of interception. This way, even if a pass was intercepted, but its projected destination classified it as line-breaking, we could still mark it as an unsuccessful line-breaking pass.
Establishing a Model to Assign Value to Passes
The initial goal of this project was to try to quantify the value of different line-breaking passes compared to those which are not, through comparing passes with similar spatial characteristics.
Ideally, an Expected Possession Value (EPV) model, embracing the abundance of tracking data available, would have been employed. Unfortunately, building a reliable, tracking-data-based EPV model is complex and would require a disproportionate amount of time compared to the benefits of the end goal.
At the other end of the scale, a non-shot expected goals model, apportioning values to events from deeper areas of the pitch, was probably too rigid for the task. Therefore, I settled on an expected possession value model similar to a VAEP framework, where event data is enhanced by the following features extracted from tracking data:
- The maximum ‘angle of view’, which is defined as the maximum angle created by the ball and any two adjacent players from the first opposition line in front of a player with the ball;

Figure 2: An example “angle of view”, displaying the area where a player in possession can pass between two opposition players within a defending line. The angle between player one, the ball and player two, marked as alpha, is the maximum angle in this scenario. The angle between player three, the ball and player four is negative and therefore is ignored in calculating the ‘line integrity’ defined in point 3 below.
-
The maximum distance between adjacent players in the first opposition line in front of the player with the ball;
-
‘Line integrity’ is defined as a sum of inverse of positive angles of view;
-
‘Line compactness’ is defined as a sum of inverse of distances between adjacent players in a line;
-
‘Pitch control’ values, at the start and the end of an action, are defined according to the model introduced in this white paper, authored by Luke Bornn and Javier Fernandez at Sloan 2018.
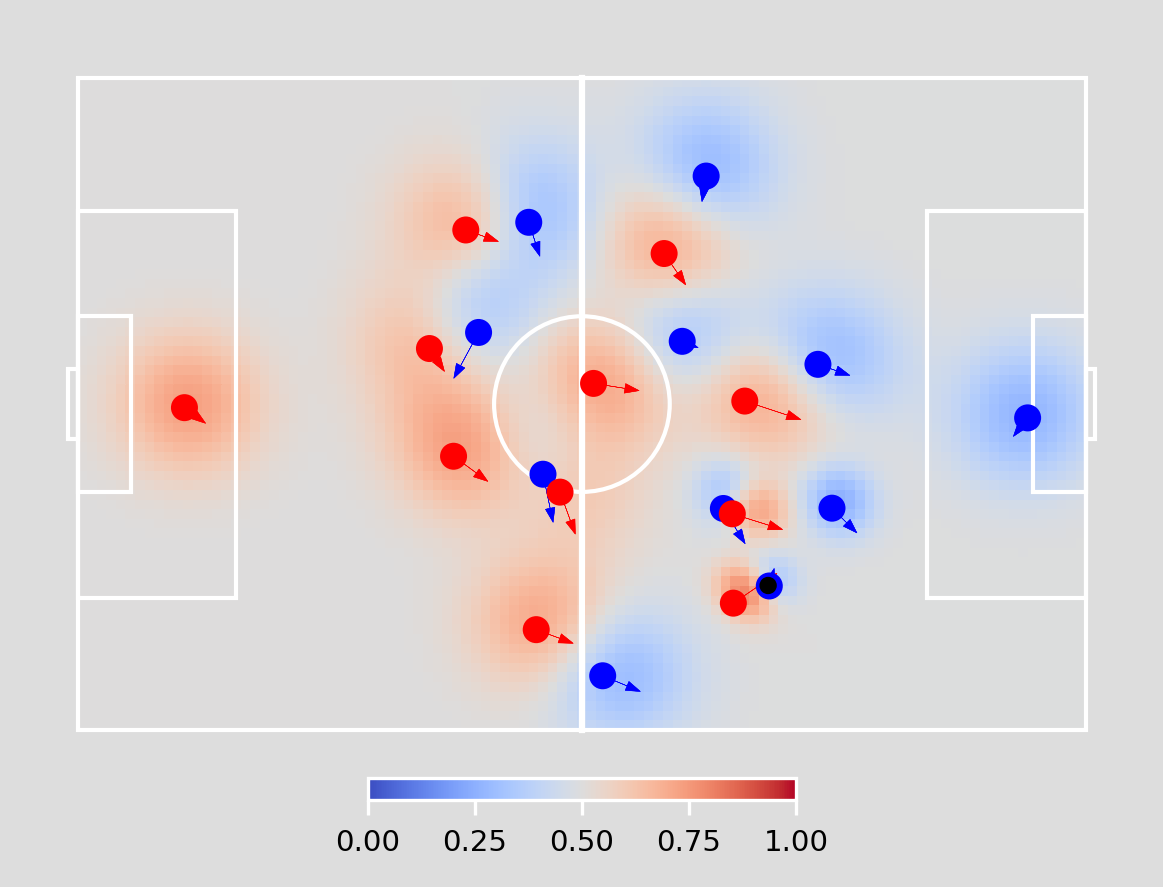
Figure 3: An example output of the ‘pitch control’ model.
Both feature one and feature two try to capture any possible vulnerability in the set-up of the line which is closest to the player in possession. The premise behind the ‘angle of view’ is that it is easier to pass the ball between two players when the angle created by those two players and the ball is bigger, either because they are set far apart from other, or because the player in possession is closer to the opposition line.
However, the distance between the adjacent players in a line is important as it is the language that many coaches use to convey their set-up to players. As a result, features three and four aim to capture the set-up of the first bank of players as a whole, applying both concepts outlined in points one and two.
When we apply a sum of inverse angles and distances to maintain the intuitive scale for both measures, low values indicate bad positioning and high values demonstrate a solid setup.
One key thing to mention is that ‘line integrity’ does not incorporate negative angles of view. Returning to the display in Figure 2, this negative angle of view is created between player three, the ball, and player four, who is effectively hidden behind the rest of the line. In this case, a potential pass could only go through those two players from the other side, breaking the line earlier between players two and three. Therefore, although the position of player four cannot be totally ignored, it is less critical than the positions of players one, two and three. As a result I chose not to incorporate negative angles in the calculation.
All five features were processed in line with the VAEP framework, which in short meant that the characteristics of the current and previous two events in a possession chain were fed into a XGBoost model to predict the probability of the team scoring or conceding a goal in the next ten actions.
Does a Line-Breaking Pass Increase Goal Probability?
The violin plot below displays prediction probabilities for scoring and conceding a goal during any of the ten events following a pass, based on whether a pass is line-breaking or not.
A wider area on a violin plot represents a higher proportion of scenarios allocated a given probability. The median probabilities are marked by the dots and the range between the 25th and 75th percentile are documented by bars.
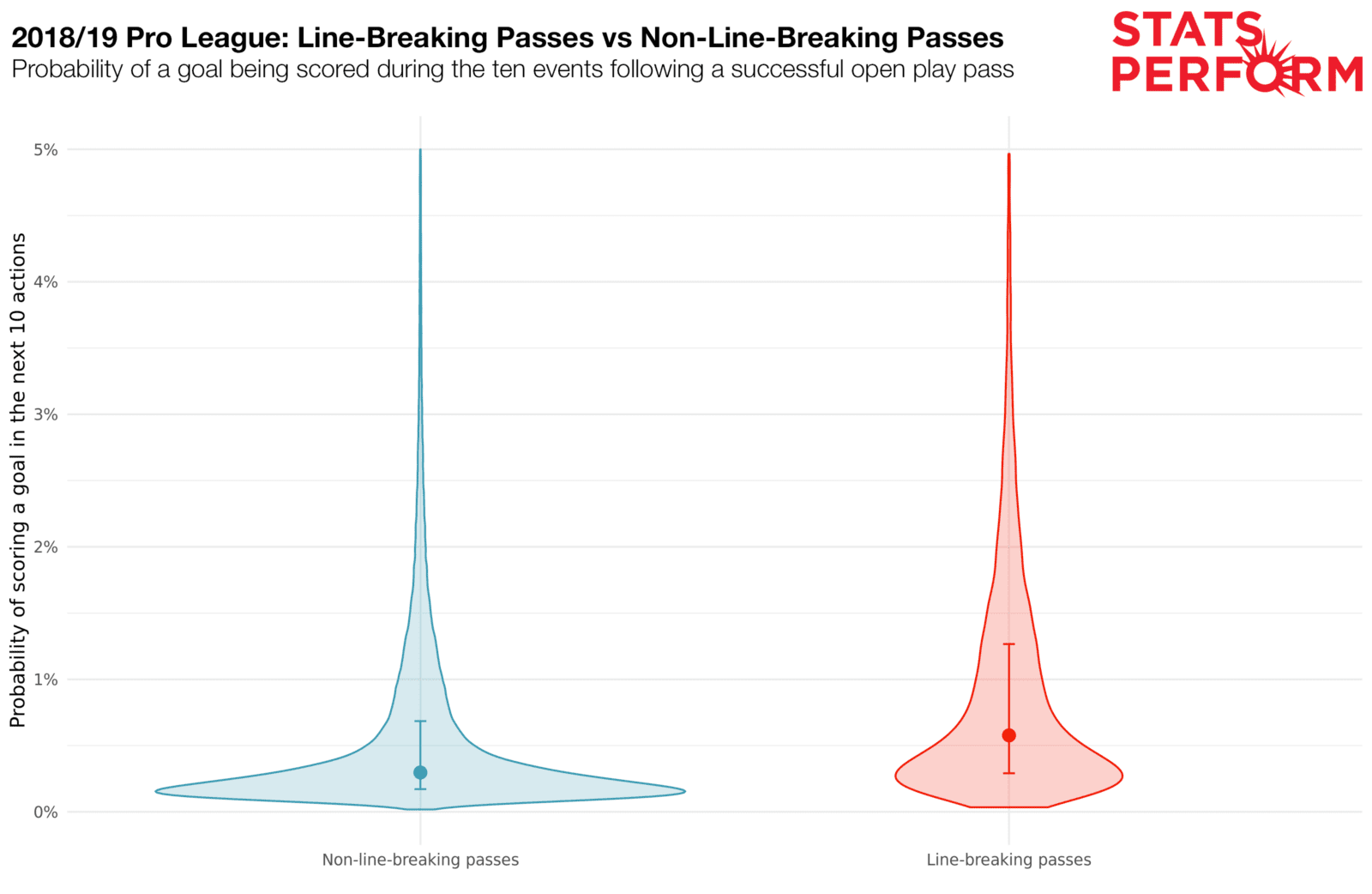
To retain a practical y-axis range, 1% of the highest probability values have been removed.
Although this approach lacks statistical rigour, it indicates that line-breaking passes boost the probability of a goal being scored, with a median value almost twice as high as non-line-breaking passes.
It is also noteworthy that an unsuccessful line-breaking pass doesn’t seem to increase the probability of a goal being conceded that much either, as highlighted below.
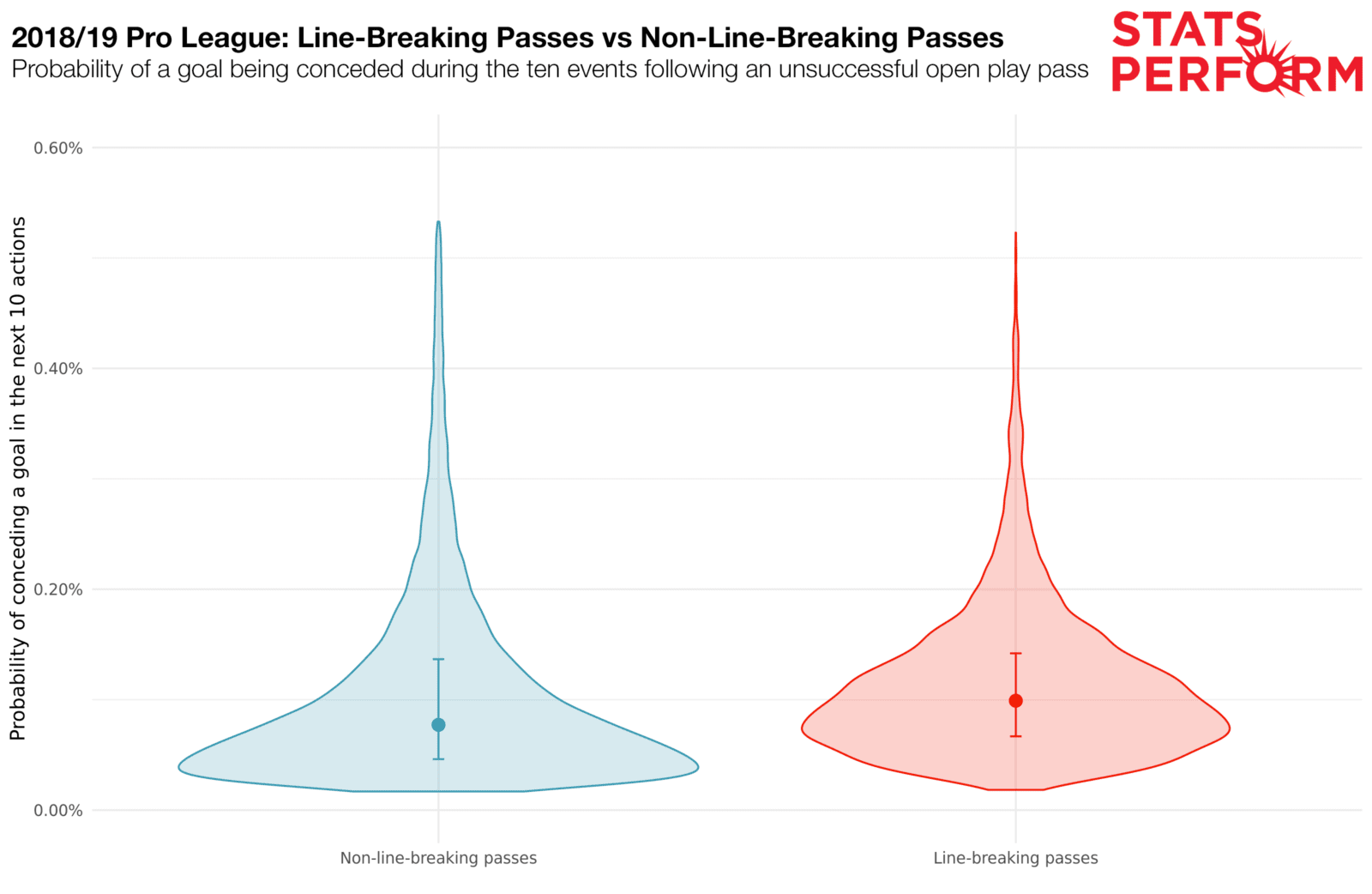
To retain a practical y-axis range, 1% of the highest probability values have been removed.
Who Were the Most Effective Players at Completing Line-Breaking Passes?
In a recruitment context, one of the benefits of defining line-breaking passes is that it can help identify prospects who are good at breaking opposition lines with a pass.
The scatter chart below plots all players who played as a central defender in at least ten matches during the 2018/19 Pro League, with the number of line breaking passes they attempted per 90 and their success rate.
The players in the top right hand quadrant scored above average in both categories.

Only players with at least 900 minutes played in central defence were included.
As with centre backs looking to play progressive passes, having the ability to transition the ball into the next attacking phase is crucial for deep-lying playmakers. The outputs for players categorised as holding central midfielders are plotted below.
One of the key standout players from last season was Ruslan Malinovskiy, who transferred from Genk to Atalanta last summer.
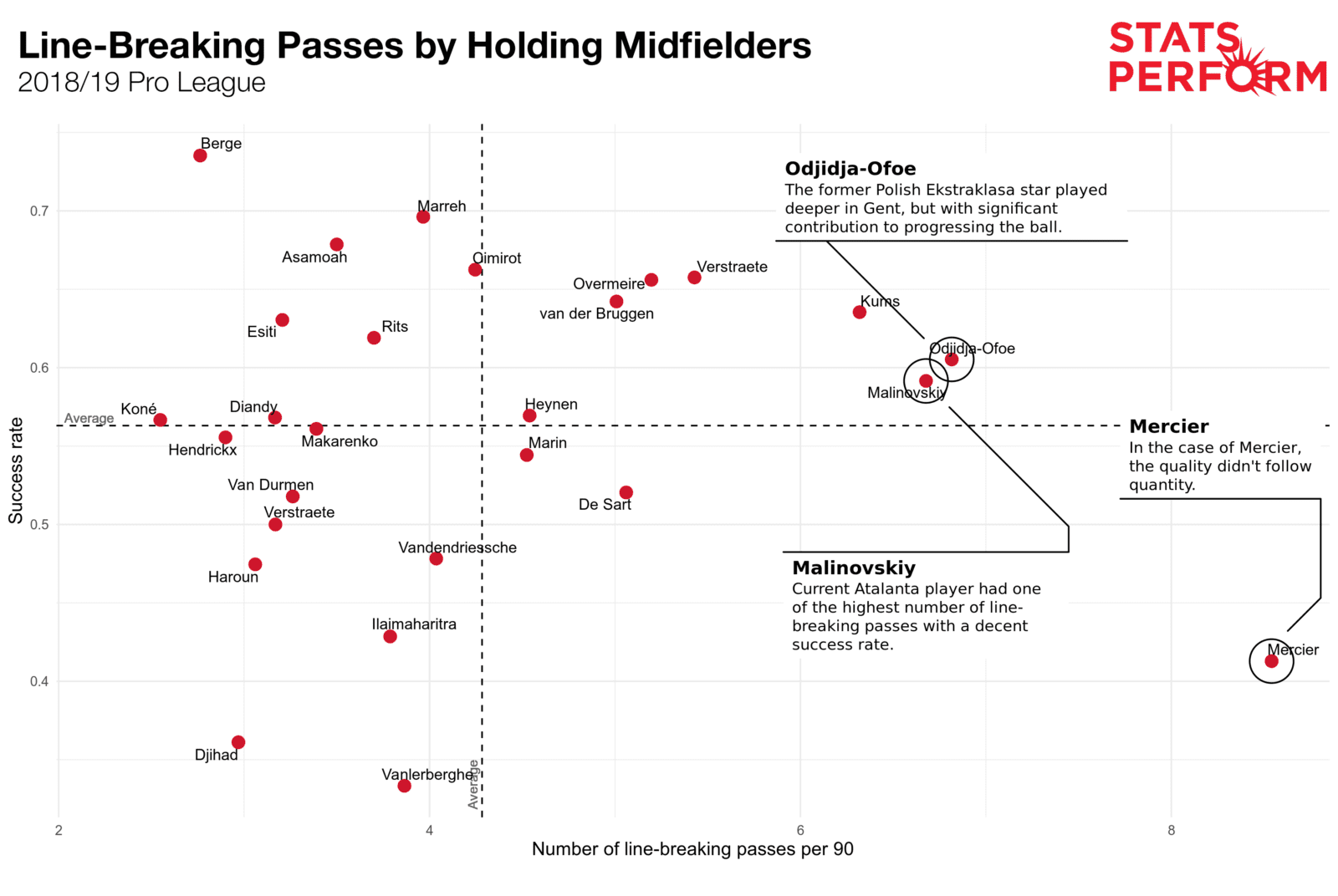
Only players with at least 900 minutes played at defensive midfield were included.
Can You Identify Line-Breaking Passes with Event Data?
Having the ability to automatically detect line-breaking passes can result in considerable workflow benefits for a video analyst, who has to spend a significant amount of time manually searching for them.
As a footnote, given the lack of availiabity of tracking data outside of a domestic competition, as part of this research I also looked to build a model that predicts if a pass was line-breaking or not based on only features derived from event data.
This model possessed an accuracy of 84% and an AUC score of 93%, which meant that the model could predict if a pass was line-breaking or not in 84 out of 100 instances.
However given that only 8% of all passes were line-breaking, the cut-off point for assigning labels was crucial. I settled on a model with a recall of 89% and precision rating of 32%, which meant that the model could correctly pick up 89% of all line-breaking passes, but at a cost of classifying many passes as line-breaking but which, in reality, didn’t actually break the line. This was to be expected, given the model cannot see where defending players are on the pitch without tracking data.
A scenario where those false positives may arise is when a team defends in a low-block and the ball is played out by the team in possession from their own defensive third into a midfielder in the opposition half, but that player is still located in front of the oppostion’s first line of defence.
Whilst this isn’t perfect, from a workflow perspective it would still narrow down the number of passes to review on video, speeding up processes and the good news is that, dependent on an analyst’s preferences, the cut-off could be adjusted to give us an even stricter classification.
The bad news is that if you want near-perfect classification of line-breaking passes without manual intervention, you still need to use tracking data.
Acknowledgments: I would like to thank Karun Singh, who read a draft version of this article and provided invaluable feedback. Moreover, thanks go to Ricardo Tavares, as well as the authors of Socceraction package, whose code was extended to prepare pitch visualisations and pre-process the data, respectively. The data used in the analysis was provided by the Belgian Pro League, captured by Stats Perform.
Appendix
The challenging goal I had in mind when kicking off with this project was to measure how much more valuable a line-breaking pass really is compared to the one that is not. My initial attempt involved the methods of Explainable Artificial Intelligence (XAI). As it turned out, an indicator feature which tells the model if a pass was line-breaking or not wasn’t particularly important to the model. At first sight, it may be something that would question their value, but I think the reality is more complicated. For obvious reasons, this ‘Is line-breaking?’ feature is highly correlated with other features like vertical distance or pitch control features. Also, the way XGBoost works made the model prefer the continuous features (like pitch coordinates, pitch control values etc.) over categorical ones (including line-breaking pass indicator), which directly impacts their importance scores. Taking only categorical variables into account, ‘Is line-breaking?’ feature was second top behind a feature that indicated if an action was open-play or set-play. Another possible approach was to use Logistic Regression instead of XGBoost to model the probabilities, which is simpler to interpret and could deliver an exact formula for the incremental in probability between a line-breaking and standard pass. However, due to the correlation with other spatial features and the complexity of the task, the quality of such a model would certainly be impacted. As a result, I settled on a visual comparison with violin plots.